|
Xc = 1/(2πfC) |
|
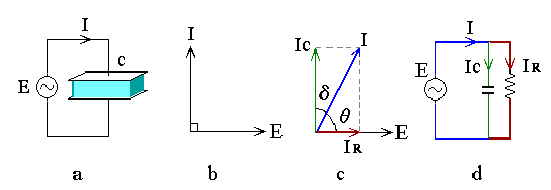
上図-a のように誘電体と1対の電極板で構成されるコンデンサの容量を C とし、
このコンデンサに交流電圧 E を印加すると、I = E× 2πfC なる電流が流れ、
同-b のベクトル図で示すように電流の位相は電圧に対して90゜進みます。 ところが、周波数が高い高周波交流では誘電体のロスにより δ だけ遅れ、 同-C のように 90゜−δ = θ だけしか進みません。 等価回路では同-d のように書き、I は IC と IR のベクトル合成されたものと考える事ができます。 このうち電圧E と同位相である IR についてP = IR × E なる発熱作用が発生します。 このδを誘電損失角、tanδ= IR/IC =1/2πfCR を誘電正接といい、誘電体である物質それぞれ固有の値をもっています。 |
|
上図-a に於いて
とすると、このコンデンサの容量は
発熱に係る電力 P は
単位体積当たりの電力を考えると
|